The 'Shroom:Issue XCIII/A Phylogenetic Analysis of the Koopas







A few months ago, I wrote an article about the evolutionary taxonomy of the Koopas, which in turn was building on an even older article I wrote about theoretical macroevolution of Koopas. My first article was about how Koopas could have evolved from dinosaurs (by way of dragons), as opposed to turtles like most folks think, with the most basal species not being quadrupedal Shellcreepers, but Bowser's species, which I call Dragon-Koopas (for lack of an official name). Having established where Koopa came from, my second article went on to explain how the diversity we see in the Mario games evolved from the draconian ancestors. Of course, my goal had been to do a proper phylogenetic analysis of the Koopas using all the real life tricks of the macroevolutionary trade, but when I codified all the traits for the 125 distinct Koopa species I recognized, it all ended up rather complicated and messy, so I oped for a general overview of the family tree instead. But while I did need to ultimately use subjective judgment calls based on a few key features in order to make a proper tree out the Koopa soup, there was a lot of science done, and actually publishing some of it is the goal of this article.
Phylogenetics 101
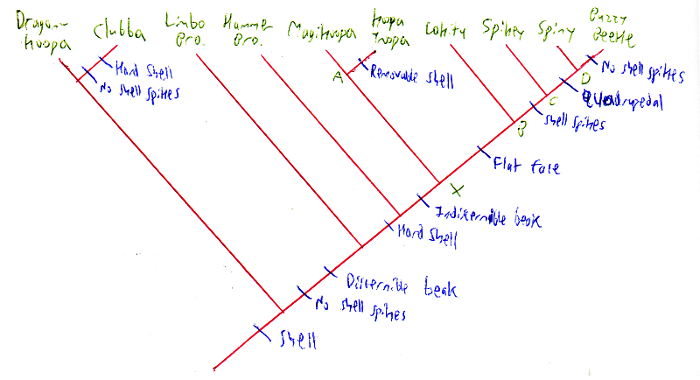
Since this article is more science-heavy than my last two evolution articles, like my Koopa genetics article, I'll start out by giving you a quick tutorial on the subject. First up is an example of a phylogenetic tree, taken straight from my previous article (but simplified a bit):
As you can see, there are three main parts of a phylogenetic tree: the species (green, like leaves), the branches that show how the species are related to each other (red), and the traits that show how the species are similar or different from one another (blue). Where branches come together are called nodes and represent the ancestors of all the species further down the tree. For example, Magikoopas and Koopa Troopas both evolved from the ancestor at the node labelled "A", while the ancestor at node X gave rise to all six of the rightmost species, as well as the ancestors at nodes A-D. These ancestors may look different from all their descendents or one of the lineages may still look exactly like the ancestor. For a real life example, fish and humans share a common ancestor, but while fish still look very much like that ancestor, our branch has changed a lot since the lineages split a few hundred million years ago. As for the Koopas, since I like to keep fanon species to a minimum, I generally assume that every ancestor does have an identical living counterpart, and that for all extensive purposes, the extant species are the same thing as the ancestral species. However, just as I make statements like "Koopa Troopas evolved from Magikoopas" to keep things simple here, in real life, we can also say things like "humans evolved from fish", even though the specific fish around today are not the same specific fish that were alive in the Paleozoic era - they're all still fish, so the point is understood.
Now, as I mentioned before, what makes species the same or different are their physical traits, which are mapped onto the phylogenetic tree at the points where traits change. For example, the "removable shell" trait on the Koopa Troopa branch indicate that the shells only became removable after they branched off from the Magikoopas, with only the Koopa Troopas possessing removable shells, while the Magikoopas and all other Koopas being unable to remove their shells. Another example is the "flat faces" trait change that occur when the Lakitus and the Spiny group split off from the Magikoopa / Koopa Troopa group: that tells us that everything below that trait change has flat faces (including the common ancestor at node "B"), while everything above it doesn't. Looking at these traits is actually how phylogenetic trees are built, including this one: I looked at all the species with flat faces and decided that the flat faces (among other traits not shown here) meant they were related, and so, I grouped them together. However, having the same traits doesn't guarantee that species are related: in this example, "hard shells" evolved from the flexible ancestral shells of the Dragon-Koopas twice, in both the Clubba branch and during the transition from Limbo Bros. to Hammer Bros. Identical characteristics that have different evolutionary origins are called homoplasious traits', and are the hated enemy of the phylogeneticists, as it makes our job harder to figure out how things are actually related with these false positives floating around. The traits we like to see are the ones that have single evolutionary origins, like the "flat face" characteristic; we call them homologous traits.
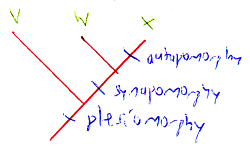
And because we like homologous traits, we're gonna talk about a few specific types of them in a bit more detail (I did say this would be a science-heavy article). The first kind are called plesiomorphies, and are traits that are shared by all the species in a tree; this is illustrated to the right, and in our example above, "shell" is a plesiomorphic trait, as all the Koopas have shells. At the other end of the spectrum are autapomorphies, which are traits that are only seen in one species in a tree, like the the Koopa Troopa's uniquely "removable shells". The third type of homologous traits are the most important to phylogeneticists: known as synapomorphies, these are traits that are shared by some, but not all the species in a tree, and can be used to determine relationships between species, like the "flat faces" example we worked through earlier. Interestingly, how closely you zoom into a tree can change the type of homologue a trait is; for example, if we zoom into the part of the tree from Hammer Bro. onward and drop out the three left species, the "hard shell" synapomorphy now becomes a plesiomorphy; or, if we zoom out and add non-Koopa dragons to the tree, the "shell" plesiomorphy becomes a synapomorphy.
The final type of homologous trait I'm going to bring up are apomorpies, which are when traits revert back to an ancestral state, such as Spikeys regaining "shell spikes" after they were lost during the transition from Dragon-Koopas to Limbo Bros. Like homoplasies, apomorphies make it look like unrelated species are actually related, which is why phylogeneticists look at as many traits as possible to find enough synapomorphies to support real relationships, rather than these sorts of false-positives. If there are too many homoplasious or apomorphic traits cluttering the data, all we are left with are polytomous bushes, where three or mode species or lineages are shown branching from single nodes, rather than nice bifurcating phylogenetic trees like our example, with two descendents per node, and at least one synapomorphic (or autapomorphic) trait change between species and nodes (except in cases where species and their ancestors are identical, like Magikoopas and ancestor "A").
Tree building 102
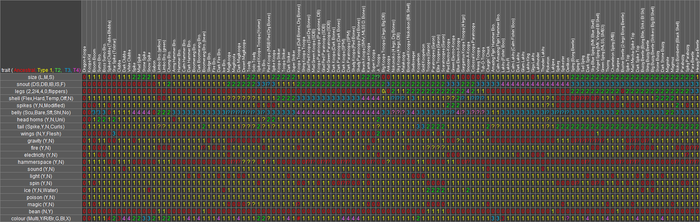
Now that we have the fundamentals and most of the terms out of the way, we can get into the details of using synapomorphies to build phylogenetic trees. So far, I've only been talking about single traits at a time, but like I said in the last paragraph and as we can see in the example, we actually need to use multiple traits to build trees. For the Koopas, I boiled down all their various characteristics into a set of 21 traits related to their physical makeup (size, shell type, stance, colour, etc.) or their supernatural abilities (fire powers, magic usage, etc.), and then codified these traits for every species, using "0" to represent the ancestral trait (i.e. whatever's seen in Dragon-Koopas), and "1"-"4" for derived traits. Bear in mind that while sometimes sequential trait evolution follows the numbers (0 --> 1 --> 2), other times, multiple traits just evolve separately (0 --> 1, 0 --> 2). I showed the full matrix in my last article, but here it is again:
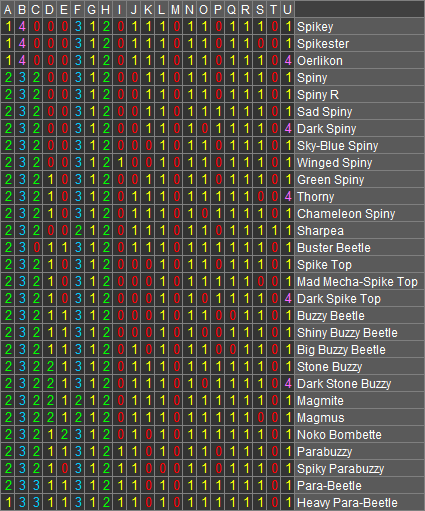
Even with my detailed tutorial as backing, it's still pretty overwhelming, so rather than tackling it all at once, what I did, and what we'll do here, is chop it up into numerous smaller parts. For our worked example, we'll use the Spiny and Buzzy Beetle group, since I was actually able to get trees out of them (rather than bushes that I then fudged into trees). Separated and transposed so that the traits are the columns (it'll be more space-efficient this way), the group looks like this:
Still rather daunting - and so we shall break it down further. But first, I'm going to quickly point out that I've converted the traits to letters. This is done not only to save space, but also because phylogenetics requires all traits to be weighted equally, rather than making speculative judgment calls like "shell structure is more important than scale colour" - which is what I admittedly did to build the overall Koopa tree out of necessity, but we're doing hard-line science in this section, and the best way to ensure neutrality is to not know what the traits are.
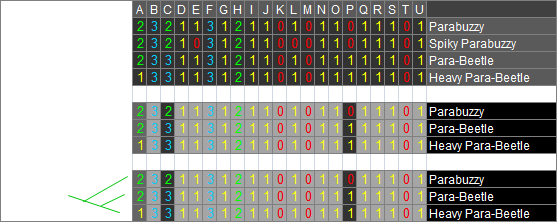
Anyway, this next step breaks down the matrix as far as it will go - into a lone set of closely related species. This is cheating a bit, since in reality, like being neutral about the traits, you should be neutral about the relationships between the species you're looking at. But even so, phylogeneticists still zero in on whatever specific groups they're studying, so we're not completely out of line. After the initial separation of our first focal group is the next step (also shown below), which is fading out the plesiomorphies and to a lesser extent, autapomorphies, so that we can focus on the synapomorphies (although only the plesiomorphies can be ignored entirely). Turns out there's only two synapomorphies and one autapomorphy, and everything agrees with each other, so the third step of drawing the tree is nice and simple:
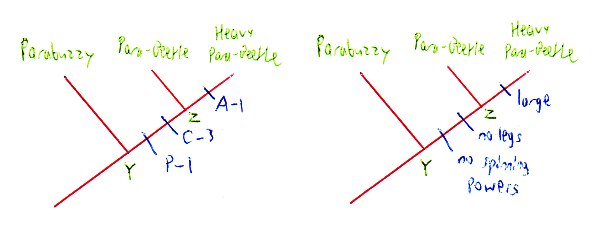
After that, the final step is mapping the traits onto the tree. The left is shorthand, using the codes (i.e. "A-1" indicates that trait A changes to state 1), while the right is with the actual traits written back in so we can see what we did. Mapping the traits let us know what the ancestors at the nodes looked like; in this case, node Y is identical to Parabuzzies and Z is identical to Para-Beetles, since there are no trait changes between those species and those nodes. Of course, this isn't always the case, and doing the Koopa trees, I did need to accept that there were a couple proto-species we haven't seen in the games (because they're extinct?) - but not in this group.
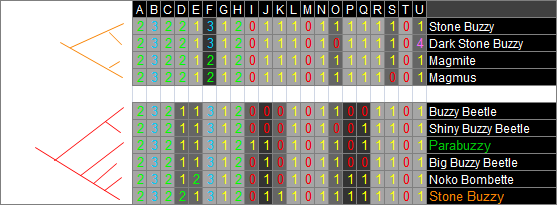
Again, this is a very simple example: it gets much harder, even in the Koopa tree, but this is just an introduction, so we'll save the hard stuff for later, and simply focus on finishing the rest of our simple Spiny tree. Following the flying Buzzy example, we can break out the rock Buzzy group, and while I'm not going to bother drawing any other traits-mapped trees, like the flying Buzzies, the ancestral node is identical to the extant Stone Buzzies. The second tree in the below image is when things get more involved, since we've clumped all the Buzzies we can and now we have to figure out how they're all related to each-other. But to keep it simple, we leave out the extra flying and rock Buzzies: we already know how they evolved from their immediate ancestors, and we also know the ancestors are identical to Stone Buzzies and Parabuzzies, so we can just use those two species to represent those chunks of the tree (once more colour-coded for convenience).
Now the wisdom of greying-out the autapomorphies as well as the plesiomorphies becomes apparent, as there are many more traits to deal with here - but only three of them synapomorphic, so it's manageable. Then, we just keep going through the rest of the group this way, with the final parts of the breakdown looking like this:
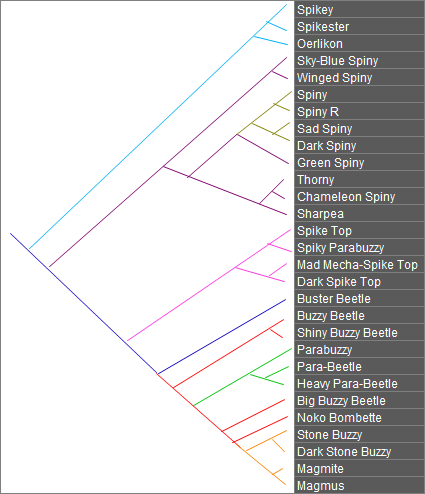
The last, dark blue tree encompasses the entire group, with most of the smaller chunks boiled down to overall representative species. Well, now the final step (since there's no way I'm gonna go to the trouble of mapping the traits onto all these trees) is expanding all those collapsed groups, giving us the full tree in all its articulated glory:
Extra credit: Optimization 103
And with that beautiful tree, this lesson draws to a close. Granted, it's been more like "A Phylogenetic Analysis of the Spiny and Buzzy Beetle family" than of the Koopa family as a whole, but that's because, I've said many times already, the rest of the tree isn't always this simple and tidy. While the only judgment calls I had to make here was related to making the initial species groupings, in other parts of the tree, I had to actively decide how species within these sorts of groups were related to each other, since the data just wouldn't agree on any one pattern in those cases. Not exactly ideal as teaching material.
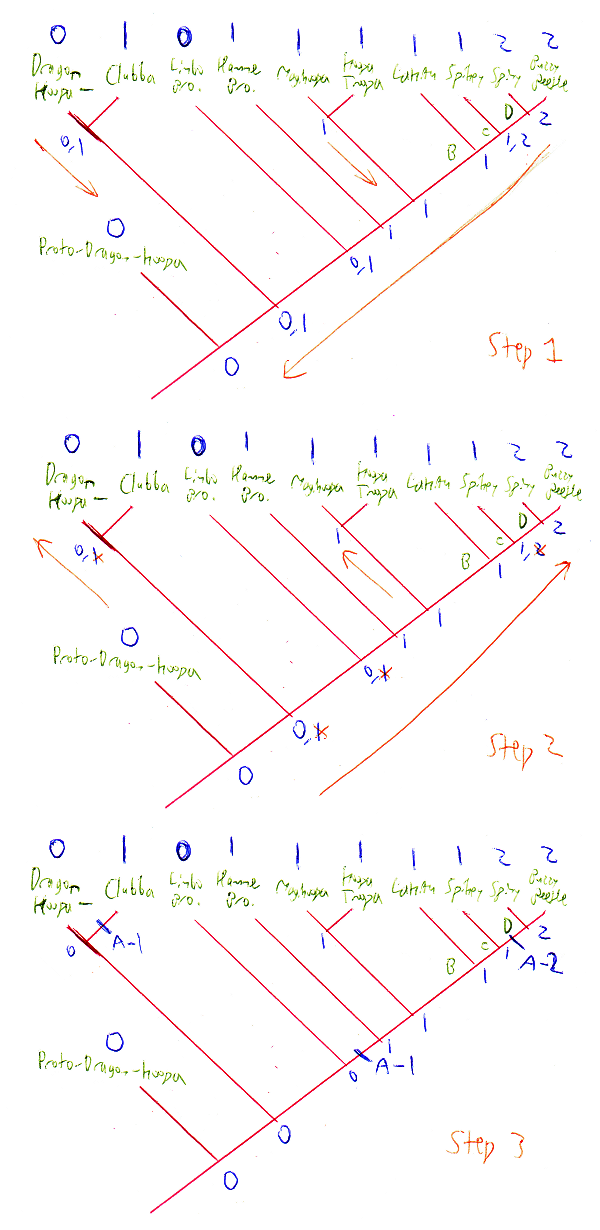
However, there are a few nice, tidy traits that can be mapped onto the Koopa summary table from the beginning of the article, so to end this on a non-Spiny/Buzzy note, I will use one of those Koooa-wide examples to quickly go over the details of mapping traits onto trees, which I only skimmed over before. The goal of any phylogenetic analysis is to use the least number of trait changes to explain the diversity of traits we see in the extant species (the simplest solution is the best solution). The tree design that requires the fewest changes is called a parsimonious tree, and basically everything I was doing with the Buzzy Beetles was aiming to create parsimonious trees for their group. However, with the overall Koopa family, the tree is already made, so all we can do is place the trait changes in the most efficient way, which is known as optimization. There are a few different ways to go about optimizing trees, but I'm just going to go over the simplest (in my opinion) strategy, which is known as ACCTRAN:
Basically, you start from the terminal ends of the branches and work your way back up the tree, using the traits of the descendents to figure out the common ancestors node-by-node. If two branches lead to species (either extant or ancestral) with the same trait, then the common ancestor at the node has that trait too (i.e. node D is labeled "2" because Spinies and Buzzies both are "2"), and you keep going no problem. But if a node gives rise to lineages with different traits, rather than saying what it has right away, you just mark it down as possibly being either one for the time being (i.e. node C originally had "1,2" written down, since Spikeys have trait type "1" and node D has "2"). Then the next node up will probably be the same as the other lineage branching off, since the equivocal node counts as both traits it might be, and majority rules (i.e. node B is "1" because Lakitus are "1" and node C counts as both "1" and "2", so it's two-to-one for "1"). Then, once you've gotten all the way to the root of the tree (this time, corresponding to the Proto-Dragon-Koopa from my original article, since the usual Dragon-Koopa-level node was ambiguous and required an outgroup to be brought in), you sweep back down through the tree and turn all the equivocals into whatever trait the node above them has (hence C's "2" got scribbled out, leaving it "1" like B).
Of course, that's just a very quick run-through of how ACCTRAN optimization works (with a bonus aside about outgroup comparison for good measure), so if you didn't quite follow this last bit, no worries - like I said, this part was just a little extra to add more Koopa to the Buzzy Beetle business. Maybe I'll do another article going into even greater depth, introducing such basic subjects as monophyletic groups and sister species to go with our knowledge about homologues and parsimonious tree construction. Assuming there's an audience for it and I'm not just talking to myself at this point, of course. But if you have stuck around until now, thank you for your time: I enjoy every minute I spend nerding it up with these Koopa macroevolution articles, and I hope you liked it too.
| Issue XCIII | |
|---|---|
| Previous Section | |